[单选题]
心形线r=4(1+cosθ),直线θ=0,θ=π/2所围图形绕极轴旋转而成旋转体的体积为()
A.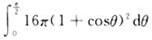
B.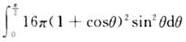
C.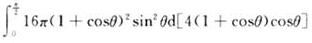
D.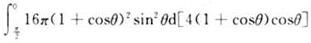
参考答案与解析:
-
相关试题
-
心形线r=4(1+cosθ),直线θ=0,θ=π/2所围图形绕极轴旋转而成旋转体的体积为()
-
[单选题]心形线r=4(1+cosθ),直线θ=0,θ=π/2所围图形绕极轴旋转而成旋转体的体积为()A.B.C.D.
- 查看答案
-
由曲线与直线x=1及x轴所围图形绕y轴旋转而成的旋转体的体积是().
-
[单选题]由曲线与直线x=1及x轴所围图形绕y轴旋转而成的旋转体的体积是().A . 3/7πB . 4/7πC . π/2D . π
- 查看答案
-
求曲线r=a(l+cosθ)(a>0)所围成的图形绕极轴旋转一周所得旋转体的体积.
-
[问答题]求曲线r=a(l+cosθ)(a>0)所围成的图形绕极轴旋转一周所得旋转体的体积.
- 查看答案
-
求曲线r=a(l+cosθ)(a>0)所围成的图形绕极轴旋转一周所得旋转体的体积.
-
[问答题]求曲线r=a(l+cosθ)(a>0)所围成的图形绕极轴旋转一周所得旋转体的体积.
- 查看答案
-
求曲线r=a(l+cosθ)(a>0)所围成的图形绕极轴旋转一周所得旋转体的体积.
-
[问答题]求曲线r=a(l+cosθ)(a>0)所围成的图形绕极轴旋转一周所得旋转体的体积.
- 查看答案
-
求y=x2与y=1,y=0所围图形绕x轴旋转的旋转体体积。
-
[问答题]求y=x2与y=1,y=0所围图形绕x轴旋转的旋转体体积。
- 查看答案
-
直线与y=H及y轴所围图形绕y轴旋转一周所得旋转体的体积为()(H,R为任意常数
-
[单选题]直线与y=H及y轴所围图形绕y轴旋转一周所得旋转体的体积为()(H,R为任意常数)。A . ['['B . πR2HC . D .
- 查看答案
-
计算由椭圆所围成的图形绕x轴旋转而成的旋转椭球体的体积为().
-
[单选题]计算由椭圆所围成的图形绕x轴旋转而成的旋转椭球体的体积为().A . B . C . D .
- 查看答案
-
曲线y=e-x(x≥0)与直线x=0,y=0所围图形绕Ox轴旋转一周所得旋转体的
-
[单选题]曲线y=e-x(x≥0)与直线x=0,y=0所围图形绕Ox轴旋转一周所得旋转体的体积为()。A . ['['B . πC . D .
- 查看答案
-
椭圆(a>b>0)绕x轴旋转得到的旋转体体积V1与绕y轴旋转得到的旋转体体积V2
-
[单选题]椭圆(a>b>0)绕x轴旋转得到的旋转体体积V1与绕y轴旋转得到的旋转体体积V2之间的关系为:()A . V1>V2B . V12C . V1=V2D . V1=3V2
- 查看答案
